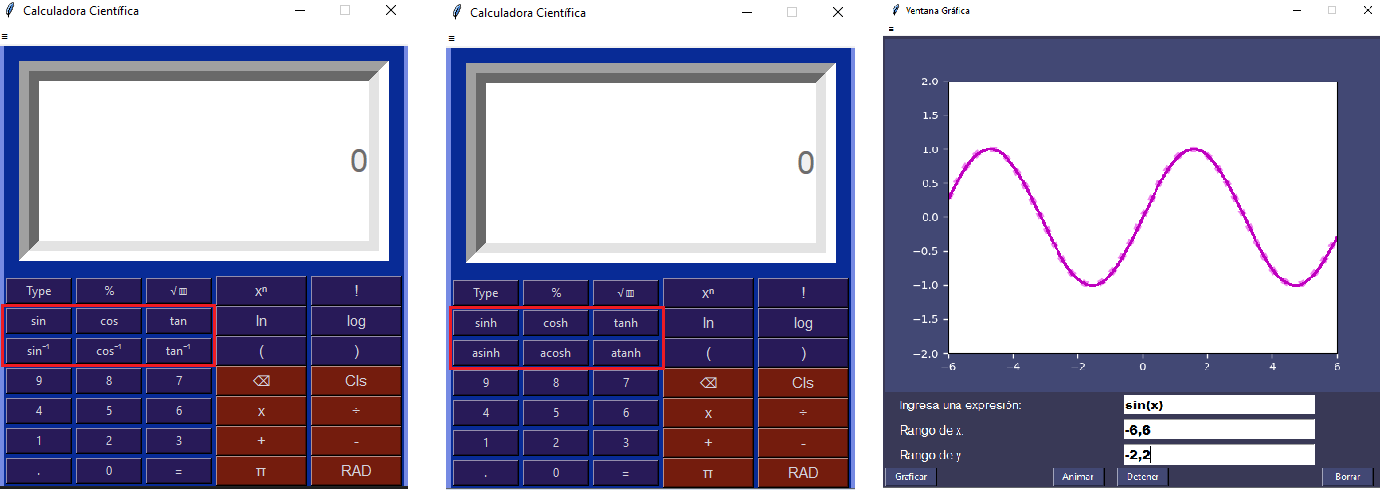
La notación polaca inversa en Python

January 31, 2022

La notación polaca inversa es uno de los algoritmos mejor desarrollados para el cálculo de operaciones aritméticas a falta de una aplicación simbólica. También se le conoce como la notación postfija, que en contraste con la forma tradicional de operar (forma infija, es decir, el operador en medio de los dos operandos), el operador aparece posterior a los operandos. El reto del día, es realizar una implementación (gráfica de ser posible) de una calculadora que utilice este algoritmo. El diseño de la calculadora es opcional y pueden utilizar las herramientas que consideren pertinentes, pero del algoritmo nos encargaremos en este post, así que vamos allá…

Contenido

Un poco de contexto historico
¿Y la teoría de grafos que tiene que ver?
La descomposición RPN
Algoritmo de implementación

Un poco de contexto historico

En 1920, Jan Lukasiewicz’ (Matemático Polaco) introdujo lo que hoy día es la notación polaca, también conocida como la notación prefija. Esta notación fue inventada con el propósito de simplificar ciertas reglas de la lógica proposicional, aunque posteriormente sería extrapolada a la aritmética, el álgebra y las ciencias de la computación, que es donde actualmente encuentra su mayor apogeo. El libro publicado por Jan demostró por primera vez que las expresiones aritméticas pueden ser especificadas sin ambigüedades dependiendo su aridad, es decir, dependiendo del número de argumentos necesarios para que dicho operador o función se pueda calcular. De esta manera, si la aridad de un operador es fija, una operación aritmética tiene como resultado una sintaxis que carece de paréntesis u otros signos de agrupación, y el operador antecede a los operandos.

Figura 1. Expresión en notación polaca inversa

La Notación Polaca Inversa (Reverse Polish Notation - RPN) o notación postfija, fue propuesta en 1954 en el artículo An Analysis of a Logical Machine Using Parenthesis-Free Notation, y como su nombre especifica ahora los operandos anteceden al operador (el caso contrario de lo que se muestra en la imagen anterior). Distintos algoritmos extendieron ambas notaciones a lo largo de los años, teniendo su primera aparición en una calculadora de sobremesa HP-9100A y posteriormente en calculadoras de bolsillo de la misma compañía. Si están interesados en conocer un poco más de esta aplicación, pueden checar el siguiente enlace que los envía a una explicación concisa sobre el uso de la notación RPN en su calculadora 12c.

Esta notación es frecuentemente utilizada en diversos lenguajes de programación que permitan incluir tipos de datos abstractos, ya que en general, la forma más sencilla de introducirla y manejarla es mediante el criterio LIFO, que optimiza los procesos a la hora de programar. La forma de implementarse puede dar lugar a una serie de ventajas y desventajas como se muestra a continuación:

Ventajas:
- El proceso que conlleva la descomposición RPN nos permite tener más control sobre los operadores y operandos.
- El hecho de que el cálculo se realice por etapas, nos permite realizar operaciones intermedias.
- También nos permite un manejo de la notación independiente de la aplicación usual de los operadores como los conocemos (más adelante hablaremos de ello).
- En términos didácticos es necesario comprender como se convierte la expresión algebraica a evaluar en su forma RPN, por lo que produce menos errores a la hora de implementarse.
- Es una aplicación directa de la teoría de grafos.
Desventajas
- Abordar la implementación por primera vez no es algo sencillo, ya que se requiere cierta practica para comprender a detalle la estructura.
- Posterior a la llegada de la notación algebraica, la notación polaca inversa fue desestimada en cuanto aplicaciones se refiere.

¿Y la teoría de grafos que tiene que ver?

Abordar la descomposición RPN precisa de conocer algunos conceptos previos involucrados en la teoría de grafos. Descomponer una operación aritmética da lugar a un tipo de grafo conocido como árbol con raíz dirigido, que al principio puede sonar un tanto extraño para aquellos que desconozcan la jerga matemática, pero nos daremos cuenta que es más intuitivo de lo que parece.

Muchas situaciones en el mundo real pueden describirse convenientemente mediante un diagrama compuesto de un conjunto de puntos, que en algunos casos se unen entre ellos mediante líneas. Un caso sencillo de visualizar es la conectividad que tenemos hoy día mediante las redes sociales (seguro asociarán la siguiente imagen con una red social bastante famosa que hasta hace poco tenía una imagen parecida en su inicio).

Figura 2. Representación de conexión entre usuarios mediante un grafo

El interés en este tipo de diagramas surge en si dos puntos están conectados (aunque de momento la forma en que estos se conectan es irrelevante), siendo entonces una abstracción matemática de este tipo de situaciones, un grafo. La definición formal es la siguiente:

Un grafo G es un par ordenado G(V(G), A(G)) que consiste en un conjunto de vértices V(G) y un conjunto A(G) de aristas (ambos disjuntos), con una función de incidencia que asocia con cada borde de G un par desordenado de vértices (no necesariamente distintos) de G. Entonces, si a es una arista (del conjunto A) y u,v son vértices (del conjunto V), tenemos que: (a)={u,v}, donde a une los vértices u,v y estos fungen como sus extremos.

La definición anterior puede parecer un tanto rebuscada, pero les aseguro que es concisa y contiene todo lo que necesitamos como punto de partida para construir una teoría al respecto. Entonces, los grafos reciben ese nombre porque pueden representarse gráficamente (¡duh!) y estas representaciones gráficas pueden ayudarnos a entender un montón de propiedades del conjunto. Solo para fijar ideas, supongamos que tenemos al grafo H compuesto de los siguientes conjuntos:

donde las relaciones están dadas según los valores que toma la función de incidencia en los distintos casos, y podemos construir la siguiente situación particular:

Esas relaciones dan paso a un sin fin de formas que el grafo podría tener, por lo que no existe un camino correcto para determinar su forma. Las posiciones relativas de los vértices y la forma que tienen las aristas generalmente no tienen tanta importancia, por lo que a continuación les muestro una posible forma que convenientemente funciona, donde los vértices son indicados por pequeños círculos y las líneas que los unen son las aristas.

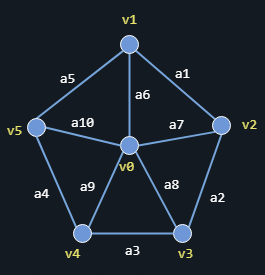
Figura 3. Posible representación del grafo mediante el conjunto de vértices y aristas

Existe una clasificación exhaustiva para cada tipo de grafo, pero no debemos perder de vista que la definición anterior es compartida para cada una de esas clasificaciones, por lo que si se entendió (conceptualmente al menos) lo anterior, abordemos un caso concreto de los grafos; los árboles. Un árbol en este contexto, hace referencia a un tipo de grafo acíclico, es decir, un grafo que no contiene ciclos (duh x2), y podemos encontrar una definición un tanto más precisa al respecto, pensando que para que un grafo pueda conectarse, debe existir al menos una ruta entre dos vértices, de forma que:

En un árbol, dos vértices están conectados exactamente por un camino

La proposición anterior es lo suficientemente intuitiva como para comprender que si nos dan el conjunto de vértices y aristas del diagrama anterior, el grafo que abordamos previamente no puede ser un árbol, ya que encontraremos que dos vértices pueden estar conectados por más de un camino. No obstante, podemos realizar las siguientes modificaciones para representar distintas situaciones en las que podemos construir un grafo de tipo árbol.

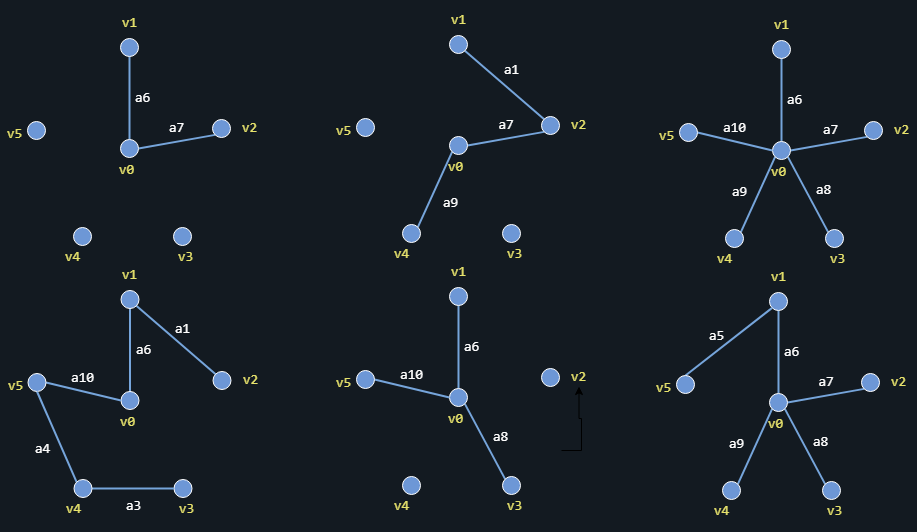
Figura 4. Arboles en distintas configuraciones

Si analizan cuidadosamente cada una de las situaciones mostradas en la imagen anterior, notarán que de los vértices utilizados, estos están conectados únicamente por un solo camino. De nueva cuenta, no hay una forma concreta de dibujar todos los posibles árboles que se pueden generar a partir de esos vértices, así que pueden dejar volar su imaginación y plantearse múltiples situaciones que satisfagan la proposición anterior.

Ahora, si ya se tiene claro porque ese grafo es llamado árbol, debemos hablar acerca de otro caso particular de estos árboles (así es, un caso particular dentro de un caso particular); el árbol con raíz. En este tipo de árbol, uno de los vértices es designado como raíz y en este caso las aristas toman una orientación natural desde o hacia la raíz. Veamos el siguiente diagrama:

Figura 5. Representación de un arbol con raíz, cuya orientación puede ser elegida a conveniencia.

Esto de tomar una orientación hace que tengamos que agregar una nueva palabra a nuestro árbol con raíz, es decir, un árbol con raíz dirigido. Hasta este punto, deben notar que la orientación en los ejemplos anteriores es irrelevante (de hecho, usualmente son grafos no dirigidos), pero en esta ocasión sí que merece la pena preguntarse para donde se orientan las aristas, ya que un recorrido por el grafo nos puede plantear dos situaciones distintas según la orientación que se tome. El estudio sobre este tipo de grafos también es extenso, por lo que si les interesa abordar con mayor formalidad y profundidad el tema, el libro Graph Theory - J.A. Bondy & U.S.R. Murty es para ustedes. De momento con esto será suficiente para entender la descomposición RPN, así que vamos allá.

La descomposición RPN

Antes de abordar la descomposición hay que tener claro como se efectúan las operaciones aritméticas y la aridad de los operadores o funciones con los que trabajaremos. Veamos la siguiente tabla:

Operador/Función	Aridad	Prioridad
+/-	Binaria	1
*/÷	Binaria	2
√, ^	Binaria	3
sin(n),cos(n),tan(n)	Unaria	3
arcsin(n),arccos(n),arctan(n)	Unaria	3

Las operaciones n-arias requieren de n operandos para poder efectuarse, y en esta tabla (aunque posiblemente se nos escapan mas operadores o funciones) pueden observar las operaciones unarias (que requieren de un solo operando) y binarias (que requieren de dos), que son las que se trabajan habitualmente. Si tienen curiosidad sobre como es una operación ternaria, recuerden que en matemáticas tenemos una representación compacta de sumas muy grandes: las series. Estas se representan mediante el símbolo de la suma Σ (me niego a llamarla “sumatoria”), y que requiere de tres operandos para poder efectuarse; donde comienza la suma, donde termina y el argumento a sumar.

La tercera columna indica la prioridad de las operaciones respecto a otras, es decir, si en una operación aritmética tenemos involucrados distintos operadores, deberemos efectuar primero aquellas operaciones con un nivel de prioridad más alto. Esto puede no resultar tan obvio, dado que en el día a día las operaciones que efectuamos o las realizamos en la calculadora o hacemos uso de símbolos que nos ayuden a priorizar las operaciones. Pongamos un pequeño ejemplo, imaginemos que tenemos que efectuar una sencilla operación que involucra dos operadores de igual prioridad:

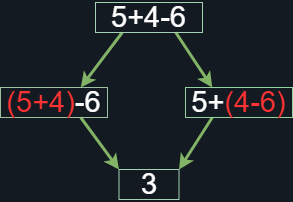
Figura 6. Operaciones con mismo nivel de prioridad

La imagen anterior indica que tenemos más de un camino para poder efectuar esa operación y dado que los operadores tienen el mismo nivel de prioridad, da igual que operación efectuemos primero, el resultado seguirá siendo el mismo (la conmutatividad a fin de cuentas). Los paréntesis nos ayudan a delimitar el “orden” en el que se efectuarán las operaciones, por tanto debemos recordar que al principio de este pequeño post, mencioné que si la aridad de los operadores es fija no hay necesidad de introducir paréntesis, y esto será importante más adelante en la implementación. No todo es color de rosa, así que vamos a plantear la siguiente operación y vamos a preguntarnos que camino es el correcto

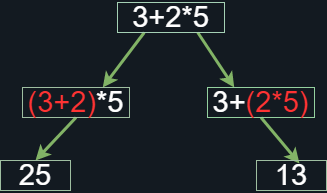
Figura 7. Operaciones con distinto nivel de prioridad

Como era de esperarse, dependiendo de la operación que decidamos efectuar primero el resultado será distinto. No debería sorprendernos que el resultado correcto es 13, ya que desde pequeños se nos enseña a priorizar las operaciones con una serie de reglas que llaman la jerarquía de operaciones. Esta jerarquía es a fin de cuentas lo que viene a representar la columna de prioridad en la tabla anterior, solo que de forma numéricamente representativa. Entonces, dado que el operador multiplicación tiene mayor prioridad sobre el operador suma, el producto debe efectuarse primero antes que la suma, y con ello el camino correcto es el de la derecha en la imagen. Con este tipo de ejemplos deberíamos ser capaces de extrapolar a los demás operadores la forma de efectuarlos, aunque aún hay que tener en consideración que existen operadores que por su naturaleza necesitan una especificación explícita sobre cual o cuales operandos se están efectuando, ya que en caso contrario, la operación puede efectuarse (a criterio del calculista) de forma errónea pero seguir siendo correcta (¿cómo?). Veamos el siguiente ejemplo para entender mejor la situación:

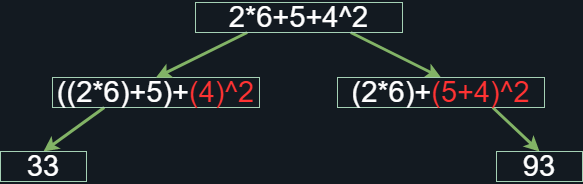
Figura 8. Operación con distintos criterios de evaluación

Como ven, ambas operaciones son correctas dado que el operador exponente requiere de dos operandos y en ambos casos los tiene. El fallo sería no especificar que operandos están involucrados en la expresión final de la base del operador exponente. Si introducimos la operación en una calculadora notaremos que el resultado final es 33. Esto sucede por que la evaluación que efectúa es secuencial, es decir, va recorriendo termino a término la expresión anterior y al no encontrar nada que sugiera que la suma 5+4 será la base que posteriormente se elevará a la potencia 2, pues simplemente evalúa únicamente al cuatro como la base.

De esta forma, podemos construir numerosos ejemplos en donde se desarrolle explícitamente la prioridad de un operador sobre otro para finalmente evaluar la expresión correctamente. Ahora vamos a abstraer esa idea planteando un árbol con raíz dirigido que descomponga la expresión aritmética en un grafo, cuyos vértices deben ser únicamente operadores u operandos. Imaginemos que tenemos la operación de la figura 6, si queremos comenzar la descomposición en un árbol con raíz dirigido, debemos designar el vértice que fungirá como raíz de nuestro árbol, este debe ser un operador. Dado que en la expresión ambos operadores tienen el mismo nivel de prioridad podemos elegir el que sea, pensemos en el operador suma, por tanto podemos separar la expresión según la figura 9:

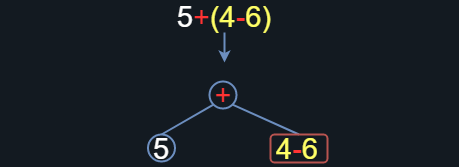
Figura 9.Construyendo el arbol con raíz dirigido asociado a la expresión arimética.

Al asignar al operador suma como raíz, tenemos dos caminos posibles a donde dirigir nuestro árbol (pues se trata de un operador binario). Por un lado tenemos como vértice al operando 5 y por otro tenemos una operación. Según lo mencionado anteriormente, los vértices únicamente pueden ser operadores u operandos, por lo que nuevamente podemos descomponer la expresión 4-6 en dos caminos con el operador resta como vértice. Entonces quedaría finalmente de la siguiente forma:

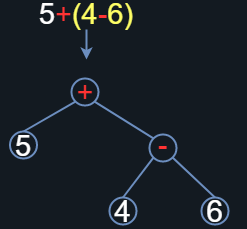
Figura 10. Arbol con raíz dirigido asociado a la expresión arimética.

La Figura 10 es el árbol con raíz dirigido asociado a la expresión aritmética. Básicamente, esta descomposición la podemos realizar con cualquier expresión que involucre n cantidad de operadores y m cantidad de operandos, cuidando las reglas de prioridad. Vamos ahora a llevar a cabo un recorrido sobre ese grafo en sentido antihorario, pasando por cada vértice del árbol y registrando nuestro paso por el sólo una vez. Si comenzamos nuestro recorrido desde la raíz, el vértice que contiene al operador suma será el primero que tocaremos, entonces lo registramos y aunque posteriormente volvamos a llegar a él, ya no se registrará de nuevo (a eso me refería con registrarlo únicamente una vez). La Figura 11 muestra el recorrido por el grafo en sentido antihorario (como indican las flechas amarillas), registrando solo una vez cada vértice por el que pasamos (las pequeñas líneas rojas que registran cuando pasamos por el vértice por primera ocasión) y el orden de recorrido (los pequeños círculos verdes enumerados.)

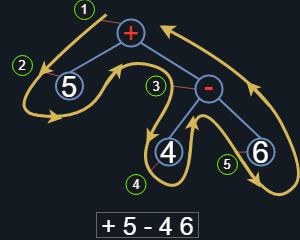
Figura 11. Recorrido por el grafo en sentido contrario a las agujas del reloj

De esta manera, como se muestra en la expresión encerrada en el rectángulo, obtenemos su representación en la Notación Polaca. Esa es una de muchas posibles representaciones de la expresión aritmética, sin embargo hay que pensar como podemos recuperar la expresión original, ya que de nada servirá esa notación si no encontramos una forma de realizar la evaluación. Para poder recuperar la expresión original tenemos la siguiente regla:

Al recorrer la expresión en notación Polaca (de izquierda a derecha), por cada operador encontrado deben existir n operandos contiguos que nos permitan efectuar la operación, en caso de ser una operación n-aria.

Entonces, en la figura 12 se describe el procedimiento realizado siguiendo esta pequeña regla, y notamos que efectivamente se recupera la expresión original.

Figura 12. La operación se efectúa cada que se encuentre un operador y dos operandos contiguos

¿Qué pasa si realizamos el recorrido en sentido horario?. Bueno, es ahí donde surge el tema del que venimos hablar principalmente; La Notación Polaca Inversa. Comencemos el recorrido ahora en sentido horario, de forma que obtendremos una expresión similar a la notación polaca, donde el paso extra será invertir la expresión generada para finalmente obtener su forma RPN. La Figura 13 muestra esta descomposición final.

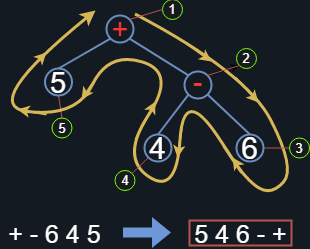
Figura 13. Recorriendo al grafo en el sentido de las manecillas del reloj, invirtiendo la expresión obtenida.

Como es natural pensar, el enunciado para recuperar la expresión original (como se muestra en la Figura 14) se ve ligeramente modificado de la siguiente forma:

Al recorrer la expresión en notación polaca inversa (de izquierda a derecha), por cada n operandos encontrados debe existir un operador contiguo que nos permita efectuar la operación, en caso de ser una operación n-aria.

Figura 14. La operación se efectúa cada que se encuentren dos operandos y un operador.

Como un pequeño resumen, la siguiente tabla muestra las consideraciones a tener al jugar con una notación u otra.

Tabla 2

Notación	Sentido de recorrido	Retorno de expresión original
Polaca	Antihorario	Por cada operador n-ario, n operandos contiguos
Polaca Inversa	Horario	Por acada n operandos, un operador n-ario contiguo

Ejercicio

Hagamos un ejercicio final que nos ayude a comprender mejor todo lo antes visto. Supongamos que tenemos la siguiente operación y queremos obtener su representación RPN.

Figura 15. Operación aritmética, cuyos operadores están representados en color rojo

Es recomendable que en este punto intenten obtener la representación RPN por su cuenta, y posteriormente vuelvan a comparar su solución. Dicho lo anterior, la descomposición mediante el árbol con raíz dirigido se ve de la siguiente forma:

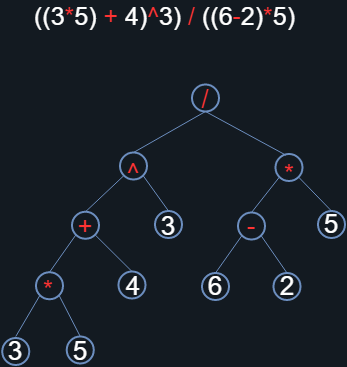
Notacion Polaca inversa a forma aritmética

Figura 16. Árbol con raíz dirigido asociado a la expresión arimética

Finalmente, al realizar el recorrido en sentido horario e invirtiendo la expresión obtenemos su representación RPN.

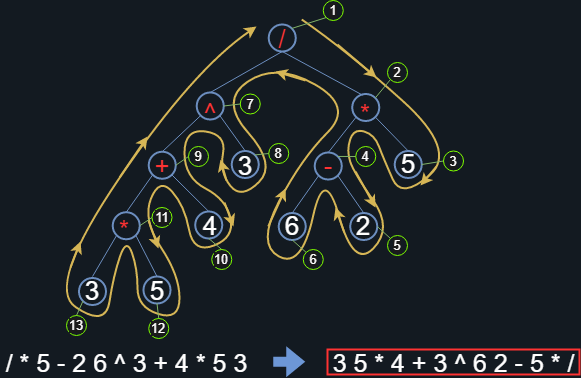
Figura 17. Árbol con raíz dirigido asociado a la expresión arimética

Queda a trabajo del lector recuperar la expresión original siguiendo la regla mostrada en la tabla anterior.

Algoritmo de implementación

Para realizar la implementación dividiré el problema en 3 partes.

Descomposición de la expresión aritmética
Construcción de expresión RPN
Evaluación de expresión RPN

Comencemos entonces con el primer punto.

1. Descomposición de la expresión aritmética

La introducción de una expresión aritmética al programa se interpreta como una cadena de texto, por lo que inicialmente no hay forma de distinguir entre operadores y operandos, ya que serán el mismo tipo de dato. El primer paso natural debería ser separar la cadena de texto en operadores y operandos, cada uno como elementos en un arreglo o introduciendo espacios entre elementos para su posterior identificación. Entonces, supongamos que tenemos la siguiente expresión aritmética ingresada en la calculadora; (5+6)*2.

Tendremos que recorrer la cadena carácter a carácter para ir identificando cuando se trata de un número y cuando se trata de algún otro símbolo. Identificar un número no es complicado, ya que estos están compuestos por dígitos, así que cualquier número (por más grande que este sea) tendrá que encontrarse en el siguiente arreglo: {0,1,2,3,4,5,6,7,8,9}. Por otro lado, los símbolos aritméticos también son una convención bastante general en distintas regiones y estos podemos delimitarlos sin mayor problema en la calculadora, es decir, podemos elegir el siguiente conjunto de operadores aritméticos: {+,-,*,/,^,(,)}, y podemos agregar más de ser necesarios. Con esto, no debería ser un problema fragmentar la cadena de texto en múltiples elementos que estarán separados como operadores y operandos. En pseudocódigo quedaría de la siguiente forma:

str expresion = "(5+6)*2" #Expresión a descomponer
str arreglo_digitos = ["0","1","2","3","4","5","6","7","8","9"] 
str arreglo_simbolos = ["+","-","*","/","^","(",")"]
str arreglo_final = [] #Arreglo vacío

#bucle que itera la expresión
Para *caracter en *expresion: 
  Si *caracter está en *arreglo_digitos:
    agregar a arreglo_final(*caracter[d]) #La letra "d" hace referencia a que es un dígito
  Si no está en arreglo_digitos estará en arreglo_simbolos:
    agregar a arreglo_final(*caracter[s]) #La letra "s" hace referencia a que es un símbolo


Salida: arreglo_final = ["(","5","+","6",")","*","2"]

El pseudocódigo anterior está muy simplificado y omite varios pasos intermedios que se deben realizar dependiendo el lenguaje en donde decidamos abordarlo. Pero algunos problemas generales que surgen (sin temor a equivocarme para todos los lenguajes de programación modernos) y que se deben de tomar en cuenta a la hora de programarlo son los siguientes:

Al recorrer la cadena esta contiene espacios (que estando en una calculadora gráfica difícilmente ocurrirá, pero no así en una de consola por ejemplo).
Aparece un número de más de un dígito. El pseudocódigo anterior únicamente contempla que se separa dígito de símbolo pero carácter a carácter. Por lo que si se ingresa un número del estilo 534 lo que hará será separar [“5”,”3”,”4”], y eso evidentemente es incorrecto.
Aparece una expresión con punto decimal. El pseudocódigo anterior no los contempla, por lo que deberemos contemplar el caso en que aparezca el carácter”.”.
Aparece alguna función trigonométrica (seno, coseno, tangente, arcoseno,…,etc) o variable (a,b,c,…,etc).

Contemplando esos problemas, les comparto una posible implementación en python utilizando funciones como map, chr, que nos devuelven la representación en carácter de los puntos de código Unicode pasados como números enteros.

Python

def Separar_Elementos(expr):
  simbolos = ["+","-","*","/","^","(",")"] #Elegimos los simbolos aritméticos
  digitos = list(map(chr, range(48,58))) #Digitos 0-9
  abc = list(map(chr, range(97,123))) #Caracteres  a-z
  lista_elementos = [] #Lista donde se agregarán los elementos
  cadena = "" #Cadena donde se irán concatenando los elementos

  for caracter in expr: #Comenzamos a recorrer la expresión caracter a caracter
    if caracter in digitos or caracter == ".": #Verificamos si es un digito o un punto (en caso de tener flotantes)
      cadena += caracter #Concatenamos los digitos, incluyendo al punto decimal
    elif caracter in abc: #Si no es un dígito puede ser una letra
      cadena += caracter
    else: #Si no es nada de lo anterior entonces será un símbolo
      if cadena == "" and caracter in simbolos: #La cadena debe estar vacía para poder almacenar al simbolo
        lista_elementos.append(caracter) #Agregamos el simbolo
      elif cadena == "":  #Si la cadena es vacía pero el simbolo es un espacio pues no hacemos nada
        pass
      else:
        lista_elementos.append(cadena) #Si la cadena no está vacía la vaciamos
        cadena = "" #Posteriormente limpiamos la cadena
        lista_elementos.append(caracter) #Agregamos el simbolo posteriormente

  if cadena != "": #Si al final de la iteración la cadena no está vacía, vaciamos su contenido
    lista_elementos.append(caracter)

  return lista_elementos

expresion = "(((3*5)+4)^3) / ((6-2)*5)"
expresion_separada = Separar_Elementos(expresion)
print(expresion_separada)

Salida ---> ['(', '(', '(', '3', '*', '5', ')', '+', '4', ')', '^', '3', ')', '/', '(', '(', '6', '-', '2', ')', '*', '5', ')']

2. Construcción de expresión RPN

Aunque su representación se construye (como vimos) mediante un grafo, la implementación no es tan directa a primera vista, por lo que para poder desarrollar un algoritmo de descomposición debemos tener en consideración varios detalles. Pensemos en realizar la implementación para un ejemplo como el de la Figura 16. Algunos inconvenientes de intentar obtener la representación en notación polaca inversa de forma “directa” (o intentando de alguna manera programa el grafo) pueden ser los siguientes:

Al descomponer la expresión inicialmente, nosotros designamos al operador que fungirá como raíz y eso en la implementación no podemos hacerlo (al menos no si deseamos implementar el código en una calculadora).
Suponiendo que eligiéramos un operador como raíz, la orientación tomaría al menos dos vertientes en donde cada uno de los elementos de la expresión tendría que ser separado en dos arreglos. Lo cual podría no ser práctico en vista de que la expresión final los contiene a todos.
El “recorrido” que tendríamos que realizar en sentido antihorario estaría limitado por la estructura que decidamos utilizar para guardar las “ramificaciones”, por lo que podría ser más complejo acceder a los elementos individuales.

Pueden existir aún más inconvenientes que pueden hacer al código muy complejo innecesariamente, por lo que debemos construir un algoritmo que nos permita iterar elemento a elemento en la expresión y de alguna manera ir acomodando los términos para obtener la expresión RPN. Verán que no es tan complicado como suena, pero para ello debemos tener claro como funciona un tipo de dato abstracto conocido como pila(stack en ingles), cuya característica principal es seguir el criterio LIFO, es decir, lo último en entrar, es lo primero en salir. Esto es realmente sencillo de visualizar por lo que no profundizaré en el concepto, aunque de cualquier forma pueden ir al siguiente enlace para conocer más al respecto y como pueden implementarlo en python.

Supongamos que tenemos la expresión mostrada en la Figura 13, 5+(4-6), cuya representación RPN según vimos es: 5 4 6 - +. Entonces, tendremos las siguientes reglas a seguir:

La estructura estará compuesta de dos pilas; una pila intermedia (que seguirá el criterio LIFO) y una pila final (que seguirá el criterio FIFO - Lo primero en entrar es lo primero en salir).
Si nos topamos con un elemento que es un operando, lo agregaremos a la pila final directamente.
Si nos topamos con un elemento que es un operador, deberemos ingresarlo a la pila intermedia teniendo las siguientes consideraciones:
- Compararemos el operador con el último elemento ingresado a la pila intermedia, y si el elemento de la pila intermedia es de mayor prioridad, entonces sacaremos al elemento de la pila intermedia y lo pasaremos a la pila final.
- El proceso anterior se repetirá hasta que encontremos un elemento en la pila intermedia que tenga menor o igual prioridad sobre el operador o que la pila esté vacía, y en cuanto alguna de esas situaciones suceda, agregaremos al operador a la pila intermedia.
Si la operación contiene paréntesis, al toparnos con el paréntesis de apertura (“(“), lo agregaremos a la pila intermedia.
Al toparnos con el paréntesis de cierre (“)”) vaciaremos cada elemento de la pila intermedia a la pila final, y nos detendremos hasta encontrar su correspondiente paréntesis de apertura.

Hagamos ahora una descripción lo mas gráfica posible para entender completamente la situación anteriormente planteada. Comenzamos creando las correspondientes pilas en donde almacenaremos los elementos, como se muestra en la Figura 18.

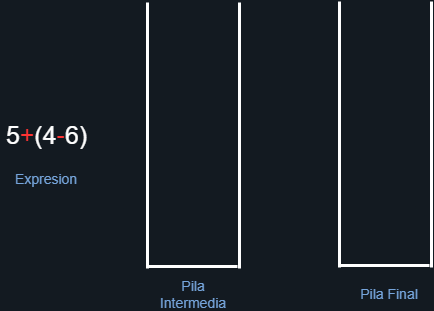
Figura 18. Creación de las pilas.

Al comenzar la iteración tenemos que el primer elemento es un operando, por lo tanto según lo anterior lo agregamos a la pila final directamente como se muestra en la siguiente imagen.

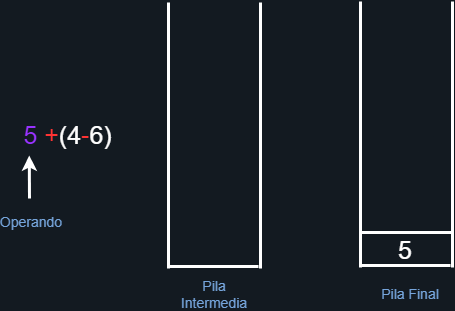
Figura 19. Anexando al operando a la pila final.

El siguiente elemento es un operador, por tanto procederemos a agregarlo a la pila intermedia que se encuentra vacía.

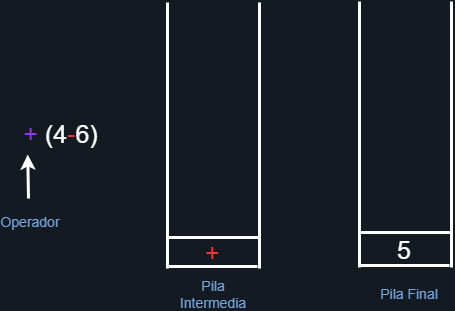
Figura 20. Anexando al operador a la pila intermedia.

Al encontrarnos con un paréntesis de apertura, lo agregamos directamente a la pila intermedia.

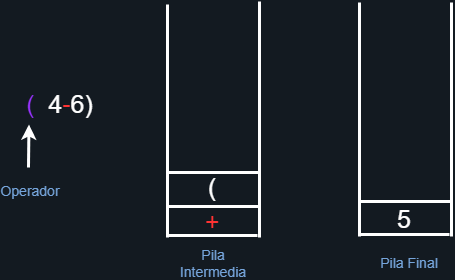
Figura 21. Agregando paréntesis de apertura a la pila intermedia.

Nuevamente nos topamos con un operando, así que lo agregamos directamente a la pila final.

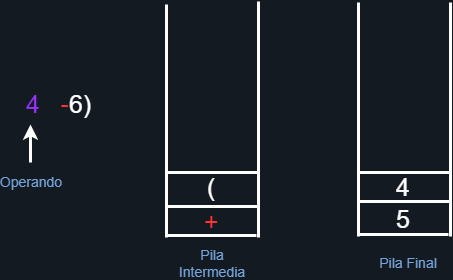
Figura 22. Anexando al operando a la pila final.

El siguiente elemento notamos que es un operador, entonces revisamos la pila intermedia y nos damos cuenta que el elemento que se encuentra hasta arriba no es de mayor prioridad (ya que nisiquiera es un operador, es el paréntesis de apertura), por tanto agregamos al operador a la pila intermedia.

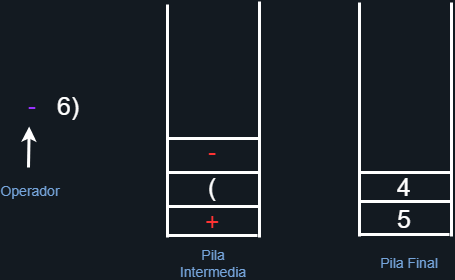
Figura 23. Agregando al operador a la pila intermedia.

Nuevamente, tenemos un operando, así que lo agregamos a la pila final.

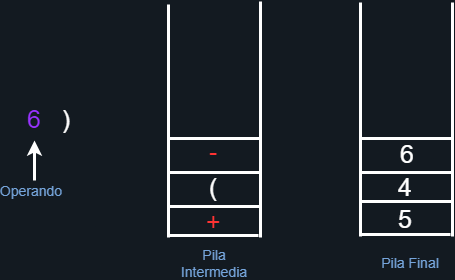
Figura 24. Agregando al operando a la pila final.

El último elemento es un paréntesis de cierre, por tanto deberemos vacíar todos los elementos de la pila intermedia a la pila final hasta encontrarnos con el correspondiente paréntesis de apertura. Los paréntesis no se agregan, lo que es igual que tirarlos a la basura.

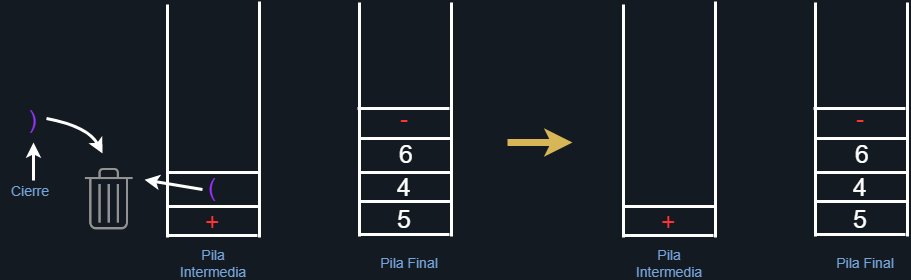
Figura 25. Recorriendo la pila intermedia hasta encontrar el parentesis de apertura.

Finalmente, al ya no tener mas elementos a iterar, revisaremos que la pila intermedia no tenga elementos. Como en este caso lo tiene (el operador suma), entonces vaciaremos ese operador a la pila final.

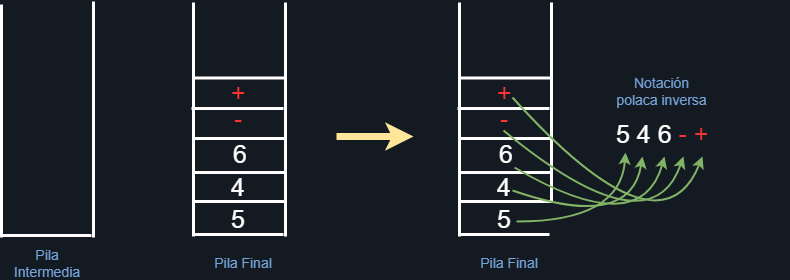
Figura 26. Vaciando elementos de la pila final.

Entonces, al vaciar la pila final nos damos cuenta que estamos obteniendo ¡la notación polaca inversa!. Aunque esto parezca bastante improvisado en realidad tiene todo el sentido del mundo. Al separar la expresión en su correspondiente grafo, notamos que el orden en la agrupación de operadores y operandos se preserva, de ahí que se separen en dos ramas iniciales, pues de esta forma nos aseguramos que las operaciones no se mezclen erróneamente entre si. Entonces, el recorrido (aunque extraño), podemos realizarlo “localmente” en cada rama del árbol, iniciando por el nodo inferior izquierdo, involucrando al nodo padre y a su (o sus) nodos hijos, siempre dejando a la raíz al final.

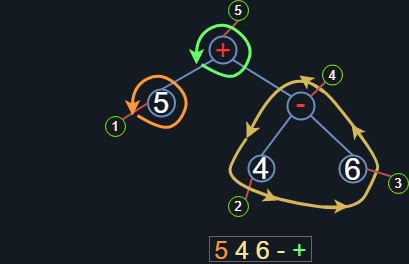
Figura 27. Recorrido por cada rama del arbol, involucrando a los nodos hijos y padres.

La expresión de la figura 15 mostrada en la sección anterior queda nuevamente como ejercicio al lector. Intentar aplicar la descomposición anterior descrita mediante pilas, y el recorrido alterno del árbol.

Siguiendo entonces la reglas mencionadas anteriormente podemos realizar la siguiente implementación en python:

def Crear_RPN(expresion):
  #Creamos un diccionario con los operadores asignandoles una cierta prioridad
  prioridad_operador = { 
        "(" : 0,
        "+" : 1,
        "-" : 1,
        "*" : 2,
        "/" : 2,
        "^" : 3
  }
  
  #Las siguiente pilas son clases previamente creadas
  #Alternativamente pueden utilizar el módulo Queue
  PilaIntermedia = Stack_LIFO() #Creamos una pila intermedia
  PilaFinal = Stack_FIFO() #Creamos una pila final

  #Comenzamos a iterar la expresión
  for elemento in expresion:
    if elemento.isdigit(): #Método para determinar si es un número
      PilaFinal.push(elemento) #Si es un número se va a la Pila Final directamente
    elif elemento == "(": #Si es un paréntesis de apertura lo agregamos directamente a la pila intermedia
      PilaIntermedia.push(elemento)
    elif elemento == ")": 
      elemento_desapilado = PilaIntermedia.pop() #Desapilamos al último elemento ingresado en la pila Intermedia
      while elemento_desapilado != "(": #Vaciamos elementos de la pila intermedia mientras no sea el paréntesis de apertura
        PilaFinal.push(elemento_desapilado)
        elemento_desapilado = PilaIntermedia.pop()
    else: #Estar aquí supone que se encontró con un caracter
      '''Si el elemento en Pila Intermedia es de mayor prioridad que el elemento de la iteración, vaciamos ese elemento a la Pila Final
      siempre y cuando la pila no esté vacía. En caso contrario, agregamos al elemento a la Pila Intermedia'''
      while (PilaIntermedia.empty() != 0) and (prioridad_operador[elemento] <= prioridad_elemento[PilaIntermedia.peek()]):
        PilaFinal.push(PilaIntermedia.pop())
      PilaIntermedia.push(elemento)
    
    #Al terminar la iteración verificamos si la pila Intermedia no tiene elementos
    #En caso de tenerlos, los vaciamos a la pila final
    while PilaIntermedia.empty() != 0:
      PilaFinal.push(PilaIntermedia.pop())
    
    return PilaFinal


Entrada: ["5","+","(","4","-", "6", ")"]
Salida: ["5","4","6","-","+"]

3. Evaluación de expresión RPN

La evaluación de la expresión es mucho más sencilla, simplemente hay que recordar el enunciado de la tabla 2 para el caso de la notación polaca inversa, de forma que por cada operador binario que encontremos, este debe estar antecedido por dos operandos. De nueva cuenta haremos uso de las pilas para ir almacenando los elementos que vayamos encontrando. Hagamos el ejemplo anterior y gráficamente mostremos su evaluación. Comenzamos iterando la expresión en RPN, de forma que nuestro primer elemento es un número, por tanto, lo agregamos a la pila de operaciones:

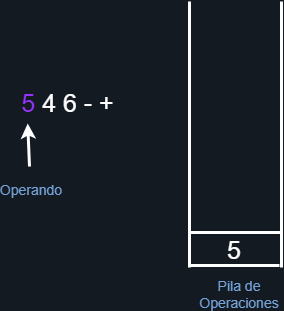
Figura 28. Agregamos el número a la pila.

Dado que los siguientes elementos también son números, los agregaremos a la pila de operaciones. Al llegar al primer operador (resta) debemos sacar de la pila a dos elementos para poder efectuar la operación en orden, y posteriormente el resultado volveremos a meterlo en la pila de operaciones.

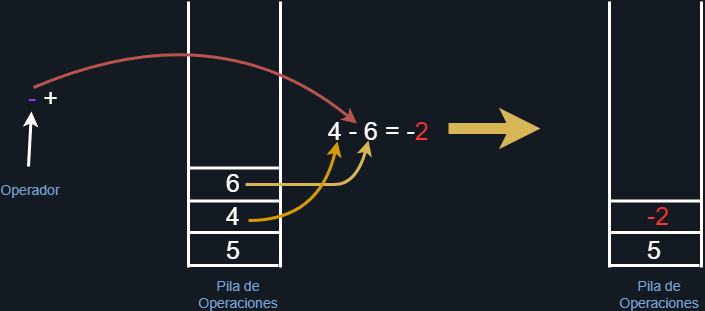
Figura 29. Por cada operador sacamos dos operandos de la pila.

Finalmente, nos volvemos a topar con otro operador (suma), por tanto, sacamos a dos elementos de la pila y los evaluamos con el correspondiente operador. De forma que al final, la pila únicamente contendrá un solo elemento correspondiente al resultado de la operación.

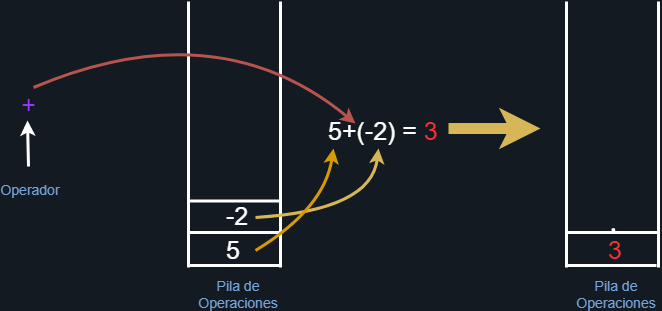
Figura 30. Evaluamos la última operación y obtenemos el resultado final.

El resultado de la operación es 3 como habíamos visto anteriormente.

La implementación en código debe tener también algunas consideraciones a la hora de programarlo.

Dado que estamos trabajando con cadenas de texto, deberemos implementar alguna especie de función de conversión que nos permita cambiar dígitos a enteros o flotantes. El detalle con eso, es que cuando en la iteración se encuentre con un operador, esta función no podrá dar su representación numérica por lo que el programa podría caer. Para ello hay que considerar capturar esa excepción.
Las operaciones tampoco podrán efectuarse directamente con el símbolo en cuestión, porque es una cadena de texto. Por ello, deberemos asociar la operación al operador del lenguaje en cuestión.
Hay que considerar el caso en el que no se ingrese una operación correcta y, por tanto, sobren operandos para operadores (o viceversa).

Dicho lo anterior, de nueva cuenta les comparto una posible implementación en python.

def Evaluacion_RPN(expresion):
  operadores = ["+", "-", "*", "/", "^"] #Operaciones a efectuar
  PilaOperaciones = Stack_LIFO() #Instancia de la pila de operaciones

  #Comenzamos a iterar la expresión
  for elemento in expresion:
    try: #Intentaremos transformar a un dato númerico 
      if "." in elemento:
        numero = float(elemento)
        PilaOperaciones.push(elemento)
      else:
        numero = int(elemento)
        PilaOperaciones.push(elemento)
    except ValueError: #Si no es posible entonces es un operador
      if elemento not in operaciones: #Si la operación no se encuentra en el compendio de operaciones
        raise ValueError(f"La operación {elemento} no es válida")

      #Si la operación se encuentra entonces sacaremos dos elementos de la pila para poder evaluarlos
      try:
        operando1 = PilaOperaciones.pop()
        operando2 = PilaOperaciones.pop()
      except IndexError: #En dado caso que ya no haya elementos por sacar
        raise ValueError("Faltan elementos a operar. La expresión ingresada no es correcta")

    #Si fue posible obtener los dos operandos de la pila, entonces efectuamos la operacion
    if elemento == operadores[0]: 
      r = e2 + e1 
    elif elemento == operadores[1]: 
      r = e2 - e1
    elif elemento == operadores[2]:
      r = e2 * e1
    elif elemento == operadores[3]:
      r = e2 / e1
    elif elemento == operadores[4]:
      r = e2 ** e1

    #Agregamos el resultado a la pila
    PilaOperaciones.push(r)

  #Una vez terminadas las iteraciones podemos devolver el resultado final que será el único elemento de la pila
  resultado = PilaOperaciones.pop()

  #Verificamos si la pila quedó vacía
  if PilaOperaciones.empty() == 0:
    return resultado
  else:
    raise ValueError("Sobran elementos a operar. La expresión no fue ingresada correctamente")


Entrada = ["5","4","6","-","+" ]
Salida = 3

Si han llegado hasta acá ¡ya tienen una forma de implementar su calculadora!. Si desean ver el algortimo en acción un tanto mas robusto y con una interfaz gráfica usando tkinter, les dejo en enlace a mi repositorio para que puedan revisar el programa. Se le agregaron algunas funcionalidades extra, como el calculo de funciones trigonométricas, inversas e hiperbólicas, además de tener las posibilidad de gráficar algunas funciones y darles una animación, en cuyo caso, los parámetros de la animación pueden elegirlos a conveniencia. Nos vemos en el siguiente post.

Mario A. Flormig