Calculo de la derivada de un Polinomio de grado n
Hoy día existen diversos programas que nos permiten realizar calculos matemáticos de todo tipo, desde una sencilla suma hasta una integral complicada. Wolfram alpha, es sin duda uno de los softwares mas poderosos actualmente con los que podemos realizar este tipo de calculos, usando procesamiento de lenguaje natural. Sin embargo, como un buen ejercicio de programación podemos realizar una implementación que derive un polinomio de grado n (determinado por el usuario) en bruto, es decir, sin la ayuda de módulos extra que realicen el cálculo por nosotros. Entonces, el reto del día es hacer ese programa, ¡vamos allá!.
Contenido
- Descomposición de la expresión en elementos
- Separación de coeficientes y exponentes
- Producto de coeficientes y exponentes
- Construcción de la derivada
- Extra: Pruebas unitarias
Descomposición de la expresión en elementos
Derivar un polinomio no es particularmente complicado, por lo que esa explicación no la abordaré con demasiados detalles y me concentraré en la implementación. No obstante, si por lo que sea necesitan recordar como se calcula, pueden revisar el siguiente enlace y posteriormente regresar para entender completamente el proceso que llevaremos a cabo a continuación.
El programa tendrá como propósito recibir una expresión que corresponda a un polinomio y posteriormente devolverá su primera derivada. Pensemos que lo que sea que vayamos a ingresar inicialmente, tendremos que tratarlo como una cadena de texto, de forma que no habrá distinción entre coeficientes, la variable y los operadores involucrados. Por ello, la primera situación natural que surge es la de separar sumandos en la expresión, para posteriormente con cada uno de ellos identificar los elementos que conforman al polinomio. Planteemos la siguiente situación particular para establecer los criterios de separación, de forma que imaginemos que en el programa introducimos el siguiente polinomio:

Figura 1. Caso partícular de un polinomio ingresado
Donde la separación debería quedar de la siguiente forma:

Figura 2. Lista cuyos elementos son los sumandos que componen al polinomio
Entonces, para poder realizar esa separación podemos realizar los siguientes pasos:
- Comenzamos a iterar carácter a carácter la cadena de texto, de forma que con ayuda de alguna variable auxiliar, iremos concatenando los correspondientes sumandos hasta encontrarnos con un signo “+” o “-“.
- Si nos encontramos con alguno de esos signos, volcaremos el contenido de la variable auxiliar en el arreglo (pues corresponderá a un sumando) y volveremos a reiniciar el valor de la variable auxiliar para la posterior concatenación de los siguientes elementos.
- Los espacios en este programa no serán tomados en cuenta.
- Al final de la iteración la variable auxiliar quedará con un último valor, correspondiente al último sumando de la expresión. Así que debemos vaciar el contenido de la variable al terminar las iteraciones.
La implementación en python podría resultar de la siguiente forma:
def Separando_Elementos(expresion):
termino = '' #Variable auxiliar donde se irán concatenando los sumandos
lista_terminos = [] #Lista que contendrá los sumandos
#Comenzamos la iteración caracter a caracter
for caracter in expresion:
if caracter == '+' or caracter == '-': #Si nos topamos con alguno de los signos entonces tendrémos un sumando que agregar a la lista
lista_terminos.append(termino) #Agregamos el sumando
elif caracter == ' ': #Ignoramos el caso en el que nos encontremos con un espacio
continue
termino += caracter #Si no es alguno de los signos o un espacio, entonces será algún otro caracter que componga al sumando
lista_terminos.append(termino) #Agregamos el sumando que se quedó al final en la variable auxiliar
return lista_terminos
Entrada: '3x^3-4x^2+x-2'
Salida: ['3x^3', '-4x^2', '+x', '-2']
Podría parecer correcto, pero los invito a introducir la siguiente expresión en el código anterior:

Figura 3. Expresión polinómica con un signo menos al inicio
Incluso sin introducirlo deberíamos de ser capaces de predecir que en la salida ¡nos agregará un carácter vacío al inicio!: [’ ‘, ‘3x^3’, ‘-4x^2’, ‘+x’, ‘-2’]. Esto sucede porque anteriormente no consideramos el caso en el que el primer carácter fuera alguno de esos signos, entonces cuando sucede, la variable auxiliar se agrega a la lista sin tener ningún valor (ya que así se declaró inicialmente). Resolver este problema puede tener diversas vertientes y dependerá del ingenio del programador en cuestión, pero como estamos aquí para resolverlo, una posible solución sería la de agregar un condicional posterior a las iteraciones, que compruebe que el carácter vacío no se encuentre en la lista. En caso de encontrarlo, estará en la primera posición, así que lo quitamos.
def Separando_Elementos(expresion):
termino = '' #Variable auxiliar donde se irán concatenando los sumandos
lista_terminos = [] #Lista que contendrá los sumandos
#Comenzamos la iteración caracter a caracter
for caracter in expresion:
if caracter == '+' or caracter == '-': #Si nos topamos con alguno de los signos entonces tendrémos un sumando que agregar a la lista
lista_terminos.append(termino) #Agregamos el sumando
elif caracter == ' ': #Ignoramos el caso en el que nos encontremos con un espacio
continue
termino += caracter #Si no es alguno de los signos o un espacio, entonces será algún otro caracter que componga al sumando
lista_terminos.append(termino) #Agregamos el sumando que se quedó al final en la variable auxiliar
#Al terminar la iteración, verificamos si hay una caracter vacio en la lista. En caso de existir estará posicionado al inicio
if '' in lista_terminos:
lista_terminos.pop(0)
Entrada: '-3x^3-4x^2+x-2'
Salida: ['-3x^3', '-4x^2', '+x', '-2']
Separación de coeficientes y elementos
Para poder identificar entre coeficientes y exponentes, será necesario acceder a los elementos de la lista de forma individual. Entonces, deberemos iterar la lista y también cada uno de sus elementos, es decir, deberemos utilizar un bucle anidado. Esto nos permitirá manejar cuando se trata de un coeficiente (porque estará antes de la variable) y cuando de un exponente (porque estará posterior a la variable).
La siguiente imagen refleja el resultado que estamos buscando.
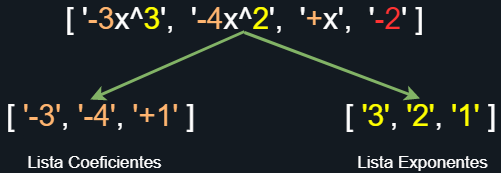
Figura 4. Listas con coeficientes y exponentes de la expresión original
Por tanto, como es costumbre, intentaré enlistar los posibles escenarios con los que tendremos que lidiar en cuanto a términos de la expresión se refiere y que a nuestro juicio consideraremos correctos. Tendremos entonces estos posibles elementos en la lista:
- Los que estan compuestos de todo; signos, coeficientes, variable, símbolo de exponente (el circunflejo “^”) y exponentes. Ejemplos: [-3x^3], [+4x^2]
- Los que no contienen signo (como podría ser el caso inicial) pero si lo demás. [3x^3], [12x^5]
- Los que no contienen signo y tampoco contienen coeficiente pero si lo demás. [x^3], [x^4]
- Los que no contienen coeficientes pero si lo demás.[+x^2], [-x^4]
- Los que no contienen exponente (el caso de orden 1) y por tanto simbolo de exponente tampoco, pero si lo demás. Ejemplos: [-3x], [+x], [-12x], [4x]
- Los que no contienen variable (caso de orden 0) y por tanto tampoco contienen simbolo de exponente ni exponentes. Ejemplos: [-2],[+100],[23]
- Los que no contienen variable (caso de orden 0) pero si contienen el simbolo de exponente y exponente. Ejemplos: [2^2] , [-4^3], [sin(90)^-2]
Seguramente se les pueden ocurrir algunos escenarios más que estén permitidos, pero de momento con estos serán suficientes para que nuestro programa pueda realizar los cálculos correctamente.
Notarán que los puntos 6 y 7 hacen referencia a los términos de orden 0, ya que pueden diferir en tener exponente o no. Esto es importante dado que el símbolo de exponente será un identificador que nos permitirá reconocer el momento en el cual guardaremos el exponente de un sumando. Entonces, dado que los términos de orden cero son constantes, su derivada será 0, y por ello no los contemplaremos en el resultado final (ya que literalmente desaparecerán de la expresión resultante).
Los puntos 5,6 y 7 podemos tratarlos como casos en la iteración que no requieren de un recorrido explícito carácter a carácter, ya que bastará con utilizar alguno de los operadores especiales que encontramos en python para identificar si los elementos contienen o no un determinado carácter. Entonces, esas primeras tres condiciones quedarían de la siguiente manera:
def Separador_coeficientes(lista_sumandos):
coeficientes = [] #Lista que contendrá los coeficientes
exponentes = [] #Lista que contendrá los exponentes
termino = '' #Variable donde se irán concatenando coeficientes o exponentes según sea el caso
for sumando in lista_sumandos:
if ('x' not in sumando and '^' not in sumando) or ('x' not in sumando and '^' in sumando): #Cualquiera de las situaciones descritas para los terminos de orden cero
continue #Simplemente no lo agregamos ya que será 0 en la derivada
elif 'x' in sumando and '^' not in sumando: #Caso para el término de orden 1
coeficientes.append(sumando[:-1]) #Nos quedamos únicamente con el coeficiente y quitamos la variable
exponentes.append("1") #Agregamos el exponente correspondiente al termino de primer orden
Para los puntos 1-4 necesitaremos un tratamiento más específico, es decir, iterando carácter a carácter para poder identificar coeficientes de exponentes en cada caso. Entonces tendremos que agregar un segundo ciclo que nos permita recorrer los caracteres del sumando en cuestión y con otras condiciones discernir cuando terminamos de recorrer el coeficiente y cuando iniciamos el recorrido del exponente.
Para entender mejor los distintos casos imaginemos que estamos iterando la expresión 3x^3-4x^2+x-2 mostrada en la figura 1. Al encontrarnos con el primer sumando (3x^3), notaremos que no entra en los casos descritos previamente, por lo que tendremos que anexarlo a una condición final. Intentaré describir los pasos a elaborar:
- Al comenzar a iterar el sumando nos encontraremos con el primer carácter 3. Por tanto, lo almacenaremos en la variable auxiliar término.
- El siguiente carácter es x, por tanto, lo anterior corresponderá al coeficiente del sumando. Entonces procederemos a guardar ese coeficiente en la lista de coeficientes y reiniciaremos el valor de la variable auxiliar. El carácter x no lo agregamos.
- Llegamos al carácter ^, lo que significa que los siguientes caracteres serán el exponente. El carácter ^ no lo agregamos.
- Al llegar nuevamente al caracter 3 (correspondiente al exponente) volvemos a almacenarlo en la variable auxiliar.
- Al ya no existir más caracteres la iteración terminará, y finalmente agregaremos el valor con el que quedó la variable auxiliar a la lista de exponentes.
Como pueden notar, el proceso descrito se tendrá que aplicar para los demás sumandos de igual forma. Entonces, podemos implementar el código de la siguiente manera:
def Separador_coeficientes(lista_sumandos):
coeficientes = [] #Lista que contendrá los coeficientes
exponentes = [] #Lista que contendrá los exponentes
termino = '' #Variable donde se irán concatenando coeficientes o exponentes según sea el caso
for sumando in lista_sumandos:
if ('x' not in sumando and '^' not in sumando) or ('x' not in sumando and '^' in sumando): #Cualquiera de las situaciones descritas para los terminos de orden cero
continue #Simplemente no lo agregamos
elif 'x' in sumando and '^' not in sumando: #Caso para el término de orden 1
coeficientes.append(sumando[:-1]) #Nos quedamos únicamente con el coeficiente y quitamos la variable
exponentes.append("1") #Agregamos el exponente correspondiente al termino de primer orden
else:
for caracter in sumando: #Comenzamos a iterar el sumando en cuestión
if caracter == 'x': #Al llegar a la x ya habrémos recorrido el coeficiente
coeficientes.append(termino) #El coeficiente recorrido lo almacenamos y reiniciamos el valor de la variable auxiliar
termino = ''
continue #Continuamos con la siguiente interación
elif caracter == '^':
continue #Continuamos con la siguiente iteración
termino += caracter #Iremos concatenando coeficiente o exponente segun sea el caso
exponentes.append(termino) #Al terminar la iteración la variable auxiliar tendrá el exponente. Lo agregamos y reiniciamos el valor de termino
termino = ''
return coeficientes, exponentes
entrada: ['3x^3', '-4x^2', '+x', '-2']
salida:
coeficientes: ['3', '-4', '+']
exponentes: ['3', '2', '1']
Como pueden observar, separa coeficientes y exponentes sin aparentes problemas (aunque si no los proponemos seguro encontraremos un problema siempre). Aun con ello, algo se nos está pasando hasta este punto. Intenten ingresar las siguientes expresiones y contrasten porque sucede lo que sucede: -x^2+2x-1, x^2+2x-1.
Si lo hicieron, notarán que las salidas que tenemos para ambos casos son las siguientes:
entrada: ['-x^2','+2x', '-1']
salida:
Coeficientes: ['-', '+2']
Exponentes: ['2', '1']
entrada: ['x^2','+2x', '-1']
salida:
Coeficientes: ['', '+2']
Exponentes: ['2', '1']
Como vemos, el caso en el que la expresión cuyo sumando inicial no contiene signo ni coeficiente, nos agrega un carácter vacío a la lista final de coeficientes. Esto no debería sorprendernos demasiado, ya que en efecto no contemplamos el caso en el que el primer término no contuviera signo o coeficiente. Esto podría ser cuestión de especificarle al usuario que agregue un signo al inicio (sea positivo o negativo) para evitar tener caracteres vacíos en la lista, porque estos ocasionarán problemas a la hora de realizar el producto exponente-coeficiente. Sin embargo, agregarle el carácter ’+’ es sencillo, en caso de que el primer sumando no lo tenga, por lo que podemos agregar una condición inicial antes de comenzar la iteración de la siguiente forma:
def Separador_coeficientes(lista_sumandos):
coeficientes = [] #Lista que contendrá los coeficientes
exponentes = [] #Lista que contendrá los exponentes
termino = '' #Variable donde se irán concatenando coeficientes o exponentes según sea el caso
#Si el signo menos no está en el primer término y además el primer caracter del primer sumando es x significará que no tiene coeficiente.
if '-' not in lista_sumandos and lista_sumandos[0][0] == 'x':
termino = '+' #Agregamos el signo
for sumando in lista_sumandos:
if ('x' not in sumando and '^' not in sumando) or ('x' not in sumando and '^' in sumando): #Cualquiera de las situaciones descritas para los terminos de orden cero
continue #Simplemente no lo agregamos
elif 'x' in sumando and '^' not in sumando: #Caso para el término de orden 1
coeficientes.append(sumando[:-1]) #Nos quedamos únicamente con el coeficiente y quitamos la variable
exponentes.append("1") #Agregamos el exponente correspondiente al termino de primer orden
else:
for caracter in sumando: #Comenzamos a iterar el sumando en cuestión
if caracter == 'x': #Al llegar a la x ya habrémos recorrido el coeficiente
coeficientes.append(termino) #El coeficiente recorrido lo almacenamos y reiniciamos el valor de la variable auxiliar
termino = ''
continue #Continuamos con la siguiente interación
elif caracter == '^':
continue #Continuamos con la siguiente iteración
termino += caracter #Iremos concatenando coeficiente o exponente segun sea el caso
exponentes.append(termino) #Al terminar la iteración la variable auxiliar tendrá el exponente. Lo agregamos y reiniciamos el valor de termino
termino = ''
return coeficientes, exponentes
entrada: ['-x^2','+2x', '-1']
salida:
Coeficientes: ['-', '+2']
Exponentes: ['2', '1']
entrada: ['x^2','+2x', '-1']
salida:
Coeficientes: ['+', '+2']
Exponentes: ['2', '1']
Producto de coeficientes y exponentes
Con las dos listas separadas, lo que queda es realizar el producto entre coeficientes y exponentes, además de restar una unidad a cada exponente de la expresión, pues recordemos que si el término es de la forma ax^n, su derivada será a*nx^(n-1).
Entonces, comenzamos planteando que necesitaremos de dos listas que contendrán los nuevos coeficientes y nuevos exponentes. Sin embargo, el primer problema que se nos presenta es ¿cómo realizaremos el producto entre coeficientes y exponentes si son cadenas de texto?. Algunos de ustedes podrían pensar: ¡Los convertimos a flotantes o enteros!, y podría ser una gran propuesta, pero si prestaron particular atención a las salidas de la función anterior, seguro notaron que algunos elementos únicamente son signos y no contienen dígitos (¿verdad que si lo pensaron?). Esto es un problema, ya que necesitamos de un dígito para que el intérprete de python pueda efectuar la “conversión” entre un tipo de dato y otro.
Con ese problema en mente les ofrezco dos alternativas: un camino en donde construimos todo a mano y otro en donde usamos a la función eval. Como al inicio de este post les prometí un camino que no necesitara de módulos extra (a pesar de que la función eval ya viene integrada y no se necesita una importación, algo dentro de mi ser me obliga a tomar el camino largo primero), pues comenzaremos con la primera alternativa. La segunda también la abordaré, pero dejaré las explicaciones profundas sobre como actúa eval para otro post.
Alternativa 1
Dado que ambas listas tienen la misma cantidad de elementos dada su construcción anterior, podemos usar la longitud de cualquiera de ellas para comenzar las iteraciones. En este caso, no es conveniente iterar directamente los elementos de una u otra, ya que necesitaremos de ambos elementos a la vez, por lo que es mejor manejar esto mediante posiciones. Entonces, construyamos esta parte inicial del código:
def Producto_coeficientes(lista_coeficientes, lista_exponentes):
nuevos_coeficientes = [] #Lista que contendrá los nuevos coeficientes, producto de la multiplicación de exponentes y coeficientes
nuevos_exponentes = [] #Lista que contendrá los nuevos exponentes, posterior a restarles una unidad
for posicion in range(len(lista_coeficientes)):
.
.
.
Ahora bien, pensemos que si nos encontramos con un elemento de la lista de coeficientes que solo contiene un signo, entonces deberemos agregarle un carácter “1”, ya que como unidad no afectará la operación, y con ello podremos realizar la conversión a tipo de dato entero o flotante según sea el caso. Esta comprobación deberemos efectuarla para cada elemento de la lista de coeficientes, puesto que pueden estar en cualquier parte de ella.
def Producto_coeficientes(lista_coeficientes, lista_exponentes):
nuevos_coeficientes = [] #Lista que contendrá los nuevos coeficientes, producto de la multiplicación de exponentes y coeficientes
nuevos_exponentes = [] #Lista que contendrá los nuevos exponentes, posterior a restarles una unidad
#Comenzamos la iteración
for posicion in range(len(lista_coeficientes)):
if len(lista_coeficientes[posicion]) == 1 and lista_coeficientes[posicion] in ['+', '-']: #Si el elemento solo contiene un caracter y es cualquiera de los signos
n_coeficiente = lista_coeficientes[posicion] + '1' #Le concatenamos un caracter '1'
else:
n_coeficiente = lista_coeficientes[posicion]
Podemos agregar algunos condicionales para determinar cuando se trata de un decimal y cuando se trata de un número entero, esto con el propósito de darles un tratamiento más “personalizado” a las operaciones y no introducir decimales cuando no se necesiten. Además, recordemos que para cada iteración tendremos un exponente que deberá valer menos una unidad, por lo que antes de terminar el ciclo deberemos restar esa unidad y agregarlo a la lista de exponentes.
def Producto_coeficientes(lista_coeficientes, lista_exponentes):
nuevos_coeficientes = [] #Lista que contendrá los nuevos coeficientes, producto de la multiplicación de exponentes y coeficientes
nuevos_exponentes = [] #Lista que contendrá los nuevos exponentes, posterior a restarles una unidad
#Comenzamos la iteración
for posicion in range(len(lista_coeficientes)):
if len(lista_coeficientes[posicion]) == 1 and lista_coeficientes[posicion] in ['+', '-']: #Si el elemento solo contiene un caracter y es cualquiera de los signos
n_coeficiente = lista_coeficientes[posicion] + '1' #Le concatenamos un caracter '1'
n_coeficiente = int(n_coeficiente) * int(lista_exponentes[posicion]) #Realizamos el producto entre el coeficiente (que será 1) y el exponente
nuevos_coeficientes.append(str(n_coeficiente)) #Anexamos el nuevo coeficiente a la lista tranformandolo nuevamente en una cadena de texto
else:
n_coeficiente = lista_coeficientes[posicion]
if '.' in n_coeficiente: #Caso en el que sea un decimal
n_coeficiente = float(n_coeficiente) * int(lista_exponentes[posicion]) #Realizamos el producto
nuevos_coeficientes.append(str(n_coeficiente)) #Agregamos el nuevo coeficiente
else:
n_coeficiente = int(n_coeficiente) * int(lista_exponentes[posicion]) #Realizamos el producto
nuevos_coeficientes.append(str(n_coeficiente)) #Agregamos el nuevo coeficiente
nuevos_exponentes.append(str(int(exponentes[posicion])-1)) #Al final del tratamiento con el coeficiente, le restamos una unidad al exponente
return nuevos_coeficientes, nuevos_exponentes
entrada:
lista_coeficientes = ['+', '+2']
lista_exponentes = ['2', '1']
salida:
nuevos_coeficientes = ['2', '2']
nuevos_exponentes = ['1', '0']
Como vemos, la salida de la función anterior sale sin problema como debería de ser (apliquen la derivada y comprueben que los coeficientes y exponentes son correctos).
Alternativa 2
Comenzaremos de forma idéntica a la alternativa anterior, pero en esta ocasión haremos uso de la función eval. Esta función recibe como argumento una cadena de texto, que analiza y evalúa como una expresión python, es decir, si python tiene la capacidad de evaluar expresiones aritméticas con lo que ingresamos (por ejemplo, en el IDLE que viene por default con la instalación), la función eval “heredará” esas capacidades. Esto es más complejo de explicar por supuesto, ya que adicionalmente la función eval puede recibir algunos parámetros más: globals y locals. Si estos argumentos no son especificados, entonces accederá al módulo builtins y este le proveerá las funciones integradas (como str(), int(), open(), etc) para ejecutar la posterior evaluación.
Sin duda, la forma de ejecutarse puede resultar interesante pero dejemoslo para otra ocasión, de momento podemos introducir la función eval de la siguiente forma:
def Producto_coeficientes(lista_coeficientes, lista_exponentes):
nuevos_coeficientes = [] #Lista que contendrá los nuevos coeficientes, producto de la multiplicación de exponentes y coeficientes
nuevos_exponentes = [] #Lista que contendrá los nuevos exponentes, posterior a restarles una unidad
#Comenzamos la iteración
for posicion in range(len(lista_coeficientes)):
if len(lista_coeficientes[posicion]) == 1 and lista_coeficientes[posicion] in ['+', '-']: #Si el elemento solo contiene un caracter y es cualquiera de los signos
n_coeficiente = eval(lista_coeficientes[posicion] + '1' + '*' + lista_exponentes[posicion]) #Le concatenamos un caracter '1', y la operación a realizar (el producto).
nuevos_coeficientes.append(str(n_coeficiente)) #Agregamos el nuevo coeficiente transformandolo a un string, ya que eval nos devolverá un dato de tipo numérico (flotante o entero según sea el caso)
else:
n_coeficiente = eval(lista_coeficientes[posicion] + '*' + lista_exponentes[posicion])
nuevos_coeficientes.append(str(n_coeficiente))
nuevos_exponentes.append(str(int(n_exponente[posicion])-1)) #Agregamos el exponente restandole 1 y posteriormente convirtiendolo nuevamente a cadena de texto
return nuevos_coeficientes, nuevos_exponentes
entrada:
lista_coeficientes = ['+', '+2']
lista_exponentes = ['2', '1']
salida:
nuevos_coeficientes = ['2', '2']
nuevos_exponentes = ['1', '0']
Como vemos, su implementación resulta en un código más corto y relativamente más sencillo de aplicar. Dentro de la función estamos construyendo la cadena de texto correspondiente al producto del coeficiente con el exponente para ambas situaciones anteriormente descritas. Aunque podría parecer una mejor implementación, no todo es miel sobre hojuelas y en ocasiones la función eval puede retornar cálculos no esperados, es decir, les recomiendo evaluar la siguiente expresión: 1.2x^3.
Salida esperada:
lista_coeficientes = ['3.6']
lista_exponentes = ['2']
Salida real:
lista_coeficientes = ['3.555555555556']
lista_exponentes = ['2']
Como ven, es una salida muy wtf. ¿Cómo resolverían ese problema? (Hint: Una solución rápida, redondeen…)
Construcción de la derivada
Estamos en la recta final de nuestro programa y con la función anterior arrojando una lista con coeficientes y otra con exponentes, lo único que resta es construir la expresión final que corresponde a la derivada. Como ya es costumbre a estas alturas, necesitaremos de una variable auxiliar en donde iremos concatenando la expresión final, luego de una serie de “filtros” que determinarán la impresión de salida del programa. En este punto la salida es un gusto personal, así que yo les mostraré una posible forma y los invito a realizar su propia salida.
- Dado que las listas tienen la misma longitud, podremos tomar la longitud de cualquiera de ellas para realizar las iteraciones correspondientes. Además, deberemos definir una variable auxiliar que irá almacenando la expresión final.
- Puede pasar que nos topemos con un exponente negativo, ya que el usuario podría ingresar expresiones de tipo ax^0, lo cuál daría como resultado un exponente -1, pero teniendo en cuenta que el producto entre el coeficiente y el exponente se anularía, el problema se reduce únicamente a evaluar si el coeficiente es cero.
- Si nos encontramos con un exponente 0, no agregaremos la variable y evidentemente el exponente tampoco.
- Si nos encontramos con un exponente 1, únicamente le agregaremos la variable sin el exponente.
- Si no es ninguno de los casos anteriores significará que el exponente es mayor que 1, entonces agregaremos la variable y el correspondiente exponente.
- Para todos los puntos anteriores habrá que agregar el signo ‘+’ para los coeficientes positivos. En caso de ser negativo se concatenará directamente.
Implementando los puntos anteriores en el código veremos que literalmente es una receta.
def Construyendo_derivada(nuevos_coeficientes, nuevos_exponentes):
expresion = '' #Variable auxiliar en donde se irá concatenando la expresion final
#Realizamos las iteraciones con base a la cantidad de elementos que contengan las listas
for posicion in range(len(nuevos_coeficientes)):
if float(nuevos_coeficientes[posicion]) == 0: #Si el coeficiente es 0, entonces no lo agregamos a la expresión final
continue
elif int(nuevos_exponentes[posicion]) == 0: #Punto 3, caso exponente cero
if '-' not in nuevos_coeficientes[posicion]: #Si no contiene el signo menos, entonces es positivo
expresion += '+' + nuevos_coeficientes[posicion]
else:
expresion += nuevos_coeficientes[posicion] #En caso contrario lo concatenamos directamente
elif int(nuevos_exponentes[posicion]) == 1: #Punto 4, caso exponente 1
if '-' not in nuevos_coeficientes[posicion]:
expresion += '+' + nuevos_coeficientes[posicion] + 'x' #Le agregamos la variable
else:
expresion += nuevos_coeficientes[posicion] + 'x'
else: #Caso con exponente mayor a 1
if '-' not in nuevos_coeficientes[posicion]:
expresion += '+' + nuevos_coeficientes[posicion] + 'x^' + nuevos_exponentes[posicion] #Le agregamos el exponente
else:
expresion += nuevos_coeficientes[posicion] + 'x^' + nuevos_exponentes[posicion]
return expresion
Entrada:
nuevos_coeficientes = ['2', '2']
nuevos_exponentes = ['1' , '0']
Salida:
expresion = '+2x+2'
Hasta este punto quizá tengan curiosidad por probar el código con distintas expresiones y ver por donde cojea. Seguramente no será complicado encontrar mas casos en donde esto falle que salgan un poco del contexto inicial de este programa, aquí les propongo algunas:
- Tener coeficientes en la expresión que no sean explícitamente números, sino que sean el resultado de aplicar una ciertas operaciones; funciones trigonométricas, exponenciales, logarítmicas, etc.
- Que los coeficientes no sean números explícitos sino letras (que al final siguen representando coeficientes que pueden tomar cualquier valor).
El primer caso es sencillo de resolver cuando se utiliza la alternativa 2 con la función eval en la parte del producto de los coeficientes con exponentes. Ya que como previamente mencioné, de no recibir los argumentos opcionales hará uso del módulo builtins y obtendrá un diccionario con variables globales, locales, funciones, etc, que tenga disponible localmente en el script. Eso significa que si nosotros importamos el módulo math, será capaz de evaluar incluso expresiones de este estilo. ¿No me creen?, adelante, agreguen las funciones del módulo e introduzcan una expresión que contenga alguna de esas funciones, y verán que no tendrá problema en evaluarlo.
El segundo caso, tampoco es un problema, ya que basta con agregar algunas modificaciones al código en la función Producto coeficientes que contemplen el caso de tener letras, y que simplemente concantenen el exponente con la letra.
Aun con todo lo anterior ¿cómo podemos estar seguros de que no se nos escapa alguna situación que si entre en el contexto del problema inicial?. Bueno, una buena costumbre es implementar pruebas a nuestras funciones que comprueben distintos casos posibles, es decir, realizando pruebas unitarias. De esta manera, estaremos menos susceptibles a errores en el programa y de identificarlos, podremos resolverlos lo antes posible. Si desean ver la implementación completa con un poco más (como también será costumbre), pueden visitar mi repositorio y enviarme sus comentarios, sugerencias y dudas.
Extra: Pruebas Unitarias
Una prueba unitaria no es más que un trozo(o trozos) de código diseñado para realizar ciertas comprobaciones sobre otro programa. Estas verificaciones pueden ser de distintos tipos, pero el propósito general es el de validar un correcto funcionamiento del programa, sometiéndolo a distintos contextos y validando que la salida sea la esperada. Esta metodología es óptima para casos concretos en los que nuestro código esté formado de distintas partes que puedan recibir una revisión individual, aunque por supuesto no es la única forma de aplicarlo pero si la más usual.
Con ello, podemos someter a todas y cada una de las funciones descritas y construidas en este post a una prueba unitaria, con la finalidad de evaluar su correcto comportamiento ante distintas situaciones. Ahora queda elegir como queremos realizar estas pruebas, es decir, podemos realizar un código ajeno al programa de forma manual que ejecute estas evaluaciones, o podemos utilizar algún módulo existente. Con ánimos de conocer nuevas herramientas, usaremos una pequeñita parte del framework unittest que se integra con la instalación de python, por lo que no deberemos realizar una instalación posterior. Este framework nos ofrece una enorme cantidad de herramientas para ejecutar pruebas de todo tipo, por lo que sus distintos tratamientos los iremos conociendo poco a poco en futuros posts.
Unittest se basa en conceptos de orientación a objetos afines a distintos lenguajes, por lo que en primera instancia, debemos elegir el tipo de prueba que queremos realizar. En nuestro caso, dado que son pequeñas funciones que únicamente devuelven objetos puntuales, elegiremos testcase (casos de prueba). La clase testcase, es una clase base que tiene como propósito verificar la respuesta de un juego particular de entradas. Esta clase funge como una interfaz que el programador implementará en una subclase y que le permitirá llevar a cabo los tests, informando los posibles fallos. Entonces, ya sea que utilicemos objetos de la clase directamente o podemos crearnos una clase particular que herede de esta clase base (que es así como se tiene pensada su implementación) y que nos permita usar sus métodos para evaluar estas entradas. Procedamos entonces con la forma recomendada, y generemos una clase (en otro script) que llamaremos TestPolinomio.
import unittest #Importamos el módulo
class TestPolinomio(unittest.TestCase): #Nuestra clase hereda de la clase TestCase
.
.
.
Ahora, el test puede contener distintas “capas”, y pensando en ello, la clase nos ofrece tres grupos de métodos que sus instancias podrán ejecutar dependiendo la información que se considere necesaria:
- El primer grupo de métodos es empleado para ejecutar los tests.
- El segundo grupo encargado de checar condiciones y reportes de fallos.
- El tercer grupo encargado de recopilar información acerca del test.
En nuestro caso particular únicamente necesitaremos un método perteneciente al primer grupo, ya que ejecutaremos el test y evaluaremos si el resultado es correcto. Por otro lado, debemos asegurarnos que el script que contiene el módulo, función o clase a probar, se encuentre debidamente importado en el script donde ejecutaremos las pruebas.
Dicho lo anterior, procederemos a construir uno o varios métodos que necesitaremos para evaluar las funciones de forma independiente o conjunta. Imaginemos que deseamos realizar pruebas a la función Separando elementos construida en la primera sección de este post. Como sabemos, recibe como entrada la expresión de un polinomio como cadena de texto y devuelve una lista cuyos elementos son los sumandos de la expresión. Para efectuar una prueba inicial, deberemos construir un método que comience con el nombre test, ya que en la ejecución de la prueba, ejecutará de manera automática todo lo que inicie así.
import unittest #Importamos el módulo
from Polinomio import Separando_Elementos #Importamos el script donde tengo la función a testear
class TestPolinomio(unittest.TestCase): #Nuestra clase hereda de la clase TestCase
def test_SeparandoElementos(self): # Método encargado de evaluar la función
.
.
.
Dentro de este método ejecutaremos uno de los muchos métodos de evaluación que nos ofrece la clase TestCase; assertEqual. Este método realizará una comparación entre la salida de la función y lo que nosotros esperamos como respuesta, de forma que recibirá dos parámetros; el primero es la ejecución de la función (teniendo en cuenta que la función debe contener un return) y el segundo el resultado esperado. De ser iguales nos devolverá un ok, y en caso contrario error, indicando la razón del porqué no son iguales.
import unittest #Importamos el módulo
from Polinomio import Separando_Elementos #Importo el script donde tengo la función
class TestPolinomio(unittest.TestCase): #Nuestra clase hereda de la clase TestCase
def test_SeparandoElementos(self): # Método encargado de evaluar la función
self.assertEqual(init.Separando_Elementos('2x^2+4'),['2x^2','+4']) #Pasamos la función como primer parámetro y el resultado esperado como segundo
Finalmente para ejecutar el test, la forma mas sencilla es usando la función main de la siguiente forma:
import unittest #Importamos el módulo
from Polinomio import Separando_Elementos #Importo el script donde tengo la función
class TestPolinomio(unittest.TestCase): #Nuestra clase hereda de la clase TestCase
def test_SeparandoElementos(self): # Método encargado de evaluar la función
self.assertEqual(init.Separando_Elementos('2x^2+4'),['2x^2','+4']) #Pasamos la función como primer parámetro y el resultado esperado como segundo
if __name__=='__main__':
unittest.main()
Salida:
----------------------------------------------------------------------
Ran 1 test in 0.000s
OK
Como vemos, la prueba fue exitosa y por tanto ese caso particular lanza un resultado correcto.
De esa manera deberemos agregar otros métodos que comprueben las otras funciones del programa. Yo les comparto una prueba que hice en general al programa completo, por si quieren agregarle más casos de uso que puedan arrojar un resultado erróneo.
import unittest #Importamos el módulo
from init import init #Importo el script donde tengo la función
class TestPolinomio(unittest.TestCase): #Nuestra clase hereda de la clase TestCase
def Test_derivada(self): # Método encargado de evaluar la función
self.assertEqual(init.init("2x^2+4"), "+4x")
self.assertEqual(init.init("-32x^4+x^3-100+4x^2+5x"), "-128x^3+3x^2+8x+5")
self.assertEqual(init.init("+7x^100 - 4x^2 +5x ^3 - 1 + 2"), "+700x^99-8x+15x^2")
self.assertEqual(init.init("- x ^2 + 2x^4 -10x + 2"), "-2x+8x^3-10")
self.assertEqual(init.init("x^3"), "+3x^2")
self.assertEqual(init.init("-2x^2"), "-4x")
self.assertEqual(init.init("-2^4 + 3x^2 - x +1"), "+6x-1")
self.assertEqual(init.init("9-6x^3"), "-18x^2")
self.assertEqual(init.init("x^5 + 7x^4 -x + sqrt(2)"), "+5x^4+28x^3-1")
self.assertEqual(init.init("- 4 x ^ 5 + 1 x ^ 2 - 100"), "-20x^4+2x")
self.assertEqual(init.init("sin(0)x^2-x + 1"), "-1")
self.assertEqual(init.init("3x^3+2x^1"), "+9x^2+2")
self.assertEqual(init.init("-5 x ^ 2 -3x^1 + 30x + 1"), "-10x-3+30")
self.assertEqual(init.init("+2.5x^2 - 1.2x^3 +10.5"), "+5.0x-3.6x^2")
self.assertEqual(init.init("3.1x^2 - 1.2x^1 +3x^0 + 2"), "+6.2x-1.2")
if __name__=='__main__':
unittest.main()
Salida:
----------------------------------------------------------------------
Ran 1 test in 0.000s
OK
Como siempre les recuerdo que los archivos pueden encontrarlos en mi repositorio y comprobar lo anterior mencionado. ¡Nos leemos en el siguiente post!